Algebra Lineal: Trabajo (modifiquen la entrada y agreguen su parte)

REPUBLICA BOLIVARIANA DE VENEZUELA

UNIVERSIDAD PEDAGOGICA EXPERIMENTAL LIBERTADOR

INSTITUTO PEDAGOGICO BARQUISIMETO

“LUIS BELTRAN PRIETO FIGUEROA”

CURSO INTENSIVO

ALGEBRA LINEAL

PROF:

MARIANA GIMENEZ

REPÚBLICA BOLIVARIANA DE VENEZUELA

UNIVERSIDAD PEDAGÓGICA EXPERIMENTAL LIBERTADOR

INSTITUTO PEDAGÓGICO “LUÍS BELTRÁN PRIETO FIGUEROA”

DEFINICION DE MATRICES Y MATRICES NOTABLES

Participantes:

María Hurtado

Tomas Sánchez

Angel Arriechi

Materia:

Algebra Lineal

Profesora:

Mariana Giménez

INTRODUCCIÓN

A través de la evolución del Álgebra lineal podemos conocer las matrices, esta la podemos definir de manera sencilla como una tabla, con m filas y n columnas de números reales ordenados (m x n) y las matrices notables son las matriz cuadradas, filas, columnas, triangulares, diagonales, entre otras.

También podemos acotar que el álgebra lineal es una rama de la matemática y que gracias a esta podemos desarrollar las habilidades lógicas para todos los seres humanos, esta rama ayuda a desarrollar el cerebro.

Con el manejo de las matrices se han creado infinidades de cosas hasta juegos didácticos para los niños y adultos de esta forma le estamos generando destreza al individuo en la lógica matemática ya que el cerebro se desarrolla, con la habilidad de sacar de manera mas rápida las cuentas y utiliza la lógica que le dará la certeza y la rapidez mental para la resolución de los problemas.

Que son Matrices

En matemática, una matriz es un arreglo bidimensional de números, y en su mayor generalidad de elementos de un anillo. Las matrices se usan generalmente para describir sistemas de ecuaciones lineales, sistemas de ecuaciones diferenciales o representar una aplicación lineal (dada una base). Las matrices se describen en el campo de la teoría de matrices.

Las matrices se utilizan para múltiples aplicaciones y sirven, en particular, para representar los coeficientes de los sistemas de ecuaciones lineales o para representar las aplicaciones lineales; en este último caso las matrices desempeñan el mismo papel que los datos de un vector para las aplicaciones lineales.

Pueden sumarse, multiplicarse y descomponerse de varias formas, lo que también las hace un concepto clave en el campo del álgebra lineal.

Ejemplo:

Podemos visitar este video en Youtube:

https://www.youtube.com/watch?v=G5PE5G7ffLY&feature=youtu.be

Definiciones de Matrices y tipos de Matrices

El concepto de Matriz es sencillo, es una tabla con m filas y n columnas de números reales ordenados (m,n∈N). Veamos una definición más matemática de las matrices Definición: se llama matriz de dimensión mxn al conjunto de números reales dispuestos en m filas y n columnas de la siguiente forma:

Definición: El conjunto de todas las matrices con m filas y n columnas se denota como Mnxm(R).

Tipos de matrices:

1. Matrices cuadradas: son las matrices que tienen igual número de filas que de columnas (m=n), y que como veremos son las únicas que pueden multiplicarse entre si. El conjunto de todas las matrices cuadradas con n filas y columnas se denotan como Mnxn(R) o Mn(R).

Elementos de las matrices cuadradas:

a. Diagonal principal: elementos de la forma aii, es decir en la diagonal que va desde a11 hasta ann.

b. Diagonal secundaria: elementos de la forma aij donde i+j=n+1, es decir los elementos en la diagonal que va desde a1n hasta an1.

Matrices triangulares superiores e inferiores: son las matrices cuadradas tal que:

a. Superior: elementos debajo diagonal de la principal son nulos aij=0 si i>j

b. Inferior: elementos encima de la diagonal principal son nulos aij=0 si i<j

Matrices Diagonales: matrices cuadradas donde todos los elementos fuera de la diagonal son cero.

Matriz Escalar: matriz diagonal en el que todos los términos de la diagonal son iguales:

Matriz Unidad o Matriz Identidad: matriz escalar cuyos elementos son 1. Se denota como I o Id:

Matriz Columna: toda matriz con una sola columna Mmx1(R)

Matriz Fila: toda matriz con una única fila M1xn(R)

Matriz Rectangular: Aquella matriz que tiene distinto número de filas que de columnas, siendo su orden m×n ,

Matriz Opuesta: La matriz opuesta de una dada es la que resulta de sustituir cada elemento por su opuesto. La opuesta de A es -A.

Matriz Nula: Si todos sus elementos son cero. También se denomina matriz cero y se denota por 0m×n

Matriz Ortogonal: Una matriz ortogonal es necesariamente cuadrada e invertible: A-1 = AT La inversa de una matriz ortogonal es una matriz ortogonal. El producto de dos matrices ortogonales es una matriz ortogonal. El determinante de una matriz ortogonal vale +1 ó -1.

Matriz Normal: Una matriz es normal si conmuta con su traspuesta. Las matrices simétricas, anti simétricas u ortogonales son necesariamente normales.

Matriz Inversa: Decimos que una matriz cuadrada A tiene inversa, A-1, si se verifica que : A·A-1 = A-1·A = I

A continuación un vídeo de profesor. ingeniero.com donde se explican los diferente tipos de matrices:

www.youtube.com/embed/dHvNlVmAm4I

Igualdad de Matrices: Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan la misma posición en ambas son iguales.

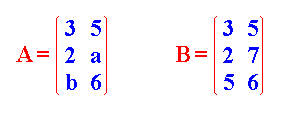
Para que las matrices A y B sean iguales, se tiene que cumplir que a = 7 y b = 5.

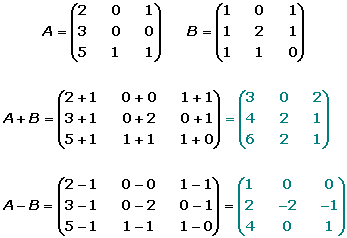
Suma de Matrices: Si las matrices A=(aij) y B=(bij) tienen la misma dimensión, la matriz suma es:

A+B=(aij+bij).

La matriz suma se obtienen sumando los elementos de las dos matrices que ocupan la misma misma posición.

Suma de matrices

Producto de Matrices

Dos matrices A y B se dicen multiplicables si el número de columnas de A coincide con el número de filas de B.

Am x n x Bn x p = Cm x p

El elemento cij de la matriz producto se obtiene multiplicando cada elemento de la fila i de la matriz A por cada elemento de la columna j de la matriz B y sumándolos.

JUEGO DE SUMA CERO ENTRE DOS PERSONAS

Este juego se conocen como juegos de suma cero entre dos personas debido a que la ganancia de un jugador es igual a la pérdida del otro y los intereses de los jugadores son completamente opuestos, por lo tanto, es suficiente con resumir el juego en términos del pago a solo uno de los dos jugadores, es decir, al designar dos jugadores A y B con estrategias m y n, respectivamente, el juego se representa mediante una matriz de pagos al jugador A, de la siguiente manera:

La anterior representación indica que si A usa la estrategia i y B la estrategia j, el pago a A es aij y el pago a B es - aij.

En la teoría de juegos se denomina jugada a la elección de una de las estrategia dadas; estas jugadas pueden ser personales, cuando la elección de la estrategia se hace conscientemente, o al azar, cuando la elección de la estrategia es realizada por un mecanismo de elección casual y no por el jugador. Para que el juego esté matemáticamente definido, se debe indicar para cada estrategia la distribución de probabilidad.

Su objetivo principal es elaborar recomendaciones para elegir la estrategia óptima, definida como la estrategia que garantiza al jugador la ganancia media máxima posible o la pérdida media máxima posible a medida que el juego se repite reiteradamente, de cada uno de los jugadores.

Estas soluciones pueden realizarse de dos formas: estrategia pura, con una sola estrategia, o estrategia mixta, con varias estrategias que se mezclan de acuerdo con probabilidades predeterminadas.

Ejemplo 1

Dos compañías A y B venden dos marcas de antigripales, La compañía A se anuncia por radio (A1), televisión (A2) y periódicos (A3). La compañía B, además de utilizar radio (B1), televisión (B2) y periódicos (B3), también manda por correo folletos (B4). Dependiendo del ingenio y la intensidad de la campaña de publicidad, cada compañía puede capturar una porción del mercado de la otra. La siguiente matriz resume el porcentaje del mercado capturado o perdido por la compañía A:

La solución del juego se basa en asegurar lo mejor de lo peor para cada jugador. Si la compañía A selecciona la estrategia A1, entonces sin importar lo que haga B, lo peor que le puede suceder es que pierda 3% de la participación del mercado a favor de B. Esto se encuentra representado por el valor mínimo de las entradas de la fila 1. De manera similar, el peor resultado de la estrategia A2 es que capture 5% del mercado de B y el peor resultado de la estrategia A3 es que pierda 9% de la participación del mercado a favor de B. Los anteriores resultados se separan en la columna “mínimo de fila” y, para lograr lo mejor de lo peor, la compañía A escoge la estrategia A2 debido a que a esta corresponde el mayor valor de la columna “mínimo de fila” denominado “Maximin”.

Considerando ahora la estrategia de B se requiere escoger el valor mínimo “Minimax” de la columna “Máximo de la columna” para lograr lo mejor de lo peor de B debido a que la matriz de pago esta dada para A. Tenemos así que la estrategia a escoger es B2.

La solución optima del juego debe seleccionar las estrategias A2 y B2, es decir, ambas compañías deben anunciarse en televisión Esto indica que el resultado estará a favor de A debido a que su participación en el mercado aumentará un 5%, por lo tanto, decimos que el valor del juego es 5% y que A y B usan una solución de punto de equilibrio. Esta solución garantiza que ninguna compañía está tentada a seleccionar otra estrategia debido a que esto ocasionaría perdidas en la participación del mercado, es decir, en caso de que B decida moverse a cualquiera de las otras estrategias, A puede escoger quedarse con la elegida ocasionando así una perdida de participación de mercado para B del 6% u 8% según la estrategia elegida por B, de igual manera, si A decide cambiar a la estrategia A3 , B puede moverse a B3 ocasionando así un incremento del 9% en la participación del mercado a favor de B.

REFERENCIAS

- http://www.vitutor.com/algebra/matrices/

- http://www.ditutor.com/matrices/

- Introducción al Algebra Lineal 5ta. Edición de Anton

ALGUNOS VÍDEOS DE MATRICES

SUMA DE MATRICES

PRODUCTO DE MATRICES

DEFINICIÓN DE MATRICES

A continuación se le presentara un vídeo el cual explicara las operaciones de matrices.para poder verlas has clic sobre esto.

Producto por Escalar

Definición:

Sea A = (aij)mxn una matriz y consideremos un escalar real . El producto de por A, el cual denotaremos como A, es la matriz de orden m x n que se obtine multiplicado cada uno de las entradas de la matriz A por el escalar Es decir: A = ( aij)mxn.