Sistema de ecuaciones lineales con Gauss Jordan

REPÚBLICA BOLIVARIANA DE VENEZUELA

UNIVERSIDAD PEDAGÓGICA EXPERIMENTAL LIBERTADOR

INSTITUTO PEDAGÓGICO “LUÍS BELTRÁN PRIETO FIGUEROA”

  

Sistema de ecuaciones lineales con Gauss Jordan

                                                                 Participantes:

Luis Torres

Rosa Freitez

Yaritza Piñero

Materia:

Algebra Lineal

Profesora:

Mariana Giménez

Definicion de Sistema de Ecuaciones Lineales:

Se le llama sistema de ecuaciones lineales a un conjunto de ecuaciones de la forma:

figura 1

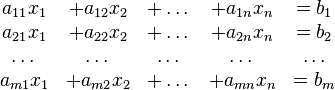
En donde x1,x2, ..., xn son las incógnitas,  b1,b2, ..., bm se denominan términos independientes y los números aij se llaman coeficientes de las incógnitas, formando una matriz que se denomina A, matriz de coeficientes. Cuando el término independiente sea cero, estamos ante un caso particular de sistemas que se conoce como  homogéneos.

Un conjunto de n números que verifiquen todas las ecuaciones se llama solución del sistema. Dado un sistema de ecuaciones, el objetivo principal es hallar todas sus soluciones, es decir, hallar todos los valores de x1,x2, ..., xn que verifican todas las ecuaciones.

¿Ahora cual es el número de soluciones?

Los sistemas de ecuaciones lineales se puede clasificar en tres tipos:

·          Sistema incompatible:  son aquellos que no poseen solución.
Ejemplo:

·          Sistema compatible:  son aquellos que poseen solución. Dentro de ellos, podemos hablar de:

·          Sistema compatible determinado: sistemas con una única solución.
Ejemplo:

·          Sistema compatible indeterminado: sistemas con infinitas soluciones.
Ejemplo:

En un sistema de ecuaciones lineales sólo se pueden encontrar estas tres situaciones, es decir, o no tiene solución, o tiene una solucion, o tiene infinitas soluciones,pero no l las tres á la vez en un mismo sistema lineal.

Teóricamente, es muy cómodo utilizar la notación matricial para un sistema. Así, todo sistema de ecuaciones lineales puede ser escrito matricialmente de la forma:

Figura 2

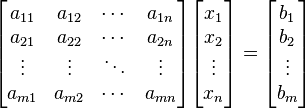
Si notamos por A es la matriz de coeficientes, x es el vector de incógnitas y b es el vector de términos independientes,y el sistema quedaría:

A x = b

Hay ocasiones en las cuales sólo es de interes saber si el sistema posee o no solución, y en caso de poseer, si es única o no.

Existe un caso particular en donde sea un sistema homogéneo:

Es cuando un sistema de ecuacion lineal de Ax=b se dice que es homogéneo si b es el vector nulo,es decir,todas la  ecuaciones están igualadas a cero:

En un sistema homogéneo,la matriz ampliada es À=(A|0),es decir,hemos añadido una columna de ceros.Por consecuencia,el rango de A coincide con el de À por lo que el sistema siempre va a ser compatible,es decir,siempre tendra solución.

Tambien se puede llegar a ese resultado mediante el razonamiento en el que en un sistema homogéneo,el cero siempre es solucion,ya que al sustituir en las ecuaciones todo sale cero,con lo cual siempre es compatible.por lo tanto cuando queramos discutir estos sistemas,solo tendremos que comprobar si el rango de A coincide con el numero de incognitas o es estrictamente menor.

Ejemplo:

https://www.youtube.com/watch?v=NMg4ArT2C5E

https://www.youtube.com/watch?v=wtSx9IJuXkM

Metodo de Gauss Jordan

El Método de Gauss Jordán o también conocido como eliminación de Gauss Jordán, es un método por el cual se pueden resolver los sistemas de ecuaciones lineales con n números de variables, encontrar matrices y matrices inversas, en este caso desarrollaremos la primera aplicación mencionada:

Para resolver sistemas de ecuaciones lineales aplicando este método, se debe en primer lugar anotar los coeficientes de las variables del sistema de ecuaciones lineales en su notación matricial:

Entonces, anotando como matriz (también llamada matriz aumentada):

Una vez hecho esto, a continuación se procede a convertir dicha matriz en una matriz en forma escalonada, es decir, una matriz equivalente a la original, la cual es de la forma:

Esto se logra aplicando a las distintas filas y columnas de las matrices simples operaciones de:

·          Multiplicar o (dividir) una fila por un número diferente de cero.

·          Sumar un multiplo de una fila a otra fila.

·          Intercambiar filas.

teniendo en cuenta que una operación se aplicara a todos los elementos de la fila o de la columna, sea el caso.

Obsérvese que en dicha matriz no aparecen los términos independientes, esto se debe a que cuando nuestra matriz original alcance la forma de la matriz escalonada, dichos términos resultaran ser la solución del sistema y se verificaran la igualdades  para cada una de las variables, correspondiéndose de la siguiente forma:

d1 = x

d2 = y

d3 = z

Ahora que están sentadas las bases, podemos explicar paso a paso la resolución de sistemas de ecuaciones lineales por medio de este método.

Para ilustrarnos mejor lo analizaremos con un ejemplo concreto:

Sea el sistema de ecuaciones:
Ejemplo 1

Resolver el siguiente sistema:

Solución:
Observar bien las operaciones en cada paso

El sistema equivalente total es:

y por lo tanto la solución del sistema es la tripleta (2, 0, -1).

Ejemplo 2:

Ejemplos en Videos:

https://www.youtube.com/watch?v=wqrQhHzCKOI